Union-find?

그래프 알고리즘의 일종으로써, 상호 배타적 집합(Disjoint Set)이라고도 한다. 여러 노드가 존재할 때, 어떤 두 개의 노드를 같은 집합으로 묶어주고, 다시 어떤 두 노드가 같은 집합에 있는지 확인하는 알고리즘이다. 아래의 2가지 연산으로 이루어져 있다.

Find: 노드 x가 어떤 집합에 포함되어 있는지 찾는 연산
Union: 노드 x와 노드 y가 포함되어 있는 집합을 합치는 연산

Union-find는 크루스칼 알고리즘에서 원소 간의 연결 여부를 판단하는 데에 사용한다.

구현

구현은 트리를 이용하며, parent[i]를 노드 i의 부모 노드라고 정의하고 초기화를 해준다. 이 때, parent[i] = i일 경우, 루트 노드임을 의미한다.

int parent[MAX_SIZE];

for (int i = 0; i < MAX_SIZE; i++) {
    parent[i] = i;
    rank[i] = 1;
}

트리의 랭크는 높이와 같은 의미를 갖지만, 아래에서 언급할 경로 압축을 사용하면 높이와 다른 값을 가질 수도 있기 때문에 높이 대신 랭크라는 표현을 사용한다. 랭크가 작은 것을 랭크가 높은 것의 자식으로 만들 것이다.

find 함수

재귀적으로 부모 노드를 찾아 루트 노드를 반환하는 함수이다. 유니온 파인드를 위해 형성된 트리는 결국 최상위 루트 노드가 자기 자신을 루트 노드로 가리키고 있기 때문에 무조건 find 함수를 종료할 수 있다.

int find(int u) {
    if (u == parent[u])    // 루트 노드
        return u;
    return find(parent[u]);
}

그러나, 위와 같이 find를 구현한 경우 문제점이 발생한다.

위 그림과 같이 한 쪽으로 트리가 치우쳐진 경우, find 함수가 루트 노드를 찾는 데 O(N)의 시간 복잡도가 걸리기 때문에 트리로 구현하는 이점이 사라진다. 이를 해결하기 위해 경로 압축 최적화를 한다.

int find(int u) {
    if (u == parent[u])    // 루트 노드
        return u;
    return parent[u] = find(parent[u]);    // 경로 압축
}

아래 그림과 같이 루트 노드인 y를 찾았으면 x의 부모를 바로 루트 노드로 바꾼다. 결과적으로 트리의 높이가 압축되어 find 함수의 효율을 높일 수 있다.

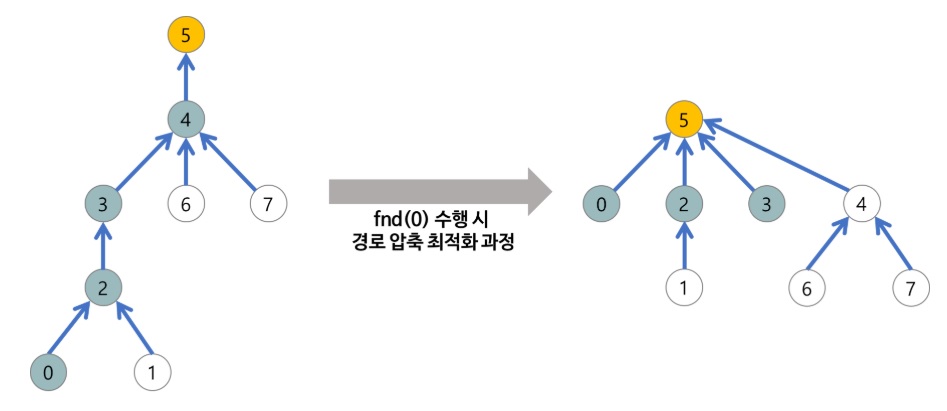
union-find-2

union 함수

union은 예약어이기 때문에 union이라는 함수명을 사용할 수 없어 보통 merge라는 이름으로 union을 표현한다. 단순히 집합을 합칠 경우, 높이가 더 높은 트리가 높이가 낮은 트리 밑으로 들어가게 되면 트리가 점점 깊어질 위험이 있다. 따라서, 트리의 높이가 낮은 트리가 높은 트리 밑으로 들어가야 하는데 이 때 rank 배열을 사용한다.

// v의 부모를 u로 만드는 함수
void merge(int u, int v) {
    // 1. 루트를 찾는다.
    u = find(u);
    v = find(v);

    // 1-1. 루트가 같다면 이미 같은 트리이므로 union할 필요 X
    if (u == v)
        return;

    // 2. 항상 u가 더 작은 트리가 되도록 하기 위해 u가 v보다 더 깊은 트리라면 swap
    if (rank[u] > rank[v])
        swap(u, v);

    // 3. u의 루트가 v가 되도록 만든다.
    parent[u] = v;

    // 4. u와 v의 깊이가 같을 때 v의 깊이를 늘려준다.
    if (rank[u] == rank[v])
        ++rank[v];
}

[참고] Weighted Union-find

위의 경우, parent 배열과 rank 배열을 둘 다 사용해야 하므로 메모리를 두 배로 사용하게 된다. 이를 개선하기 위해 Weighted Union-find 방식이 고안되었다. 이 방식에서 parent 배열이 음수일 경우, 해당 노드는 부모노드로서 음수의 절댓값이 rank가 되고, 앙수일 경우 부모 노드를 가리킨다.

예를 들어 parent[2] = -3일 경우, 2번 노드 밑에 두개의 노드가 더 있어서 총 3개의 노드가 존재한다는 의미이고, parent[3] = 5일 경우 3번 노드의 부모가 5번 노드라는 의미이다.
int parent[MAX_SIZE];

for (int i=0; i<MAX_SIZE; i++)
    parent[i] = -1;

int find(int u){
    if (parent[u] < 0) return u;
    return parent[u] = find(parent[u]);
}

void union(int u, int v){
    x = find(u);
    y = find(v);

 if (u == v)
     return;

 // parent[u], parent[v] 값은 음수이므로
 // 값이 작은 경우가 더 높이가 큰 노드이다.
    if (parent[u] < parent[v]) {
        parent[u] += parent[v];
        parent[v] = u;
 }
 else {
     parent[u] += parent[v];
     parent[v] = u;
 }
}

시간 복잡도

유니온 파인드의 시간 복잡도는 구하기가 꽤 까다롭다. 최적화 여부, 순서 등에 따라 매번 달라지기 때문이다. 코드를 살펴보면 전체 시간 복잡도와 Union 함수의 시간 복잡도는 Find 함수의 시간 복잡도에 따라 결정되는 것을 알 수 있다.

경로 압축 최적화를 하지 않은 경우, 트리가 한 쪽으로 치우칠 수 있기 때문에 Find 함수의 시간 복잡도는 최악의 경우 O(N)이다. 경로 압축 최적화를 한 경우, 트리가 짧고 넓은 형태가 될 가능성이 높아지므로 O(logN) 정도로 생각할 수 있겠다.

실제 시간 복잡도는 O(α(N))라고 한다. α(x)는 애커만 함수라고 하는데, x가 2의 65536제곱일 때 함수 값이 5가 된다. 따라서, 그냥 상수라고 봐도 무방하다.

티스토리

[알고리즘] 유니온 파인드 : Union-Find (Disjoint Set)

[알고리즘] 유니온 파인드 : Union-Find (Disjoint Set)

Union-find?

구현

find 함수

union 함수

시간 복잡도

추천 문제